Cooperative Cut

This is the reference implementation of cooperative cut. A tech report and extensions to the model are coming soon!

Cooperative cut is an inference method for Markov Random Field (MRF) problems that solves a class of higher-order energy functions by fast submodular optimization that encourages homogenous label transitions. For image segmentation, this means cooperative cut encourages coherent boundaries. In practice this can help with difficulties due to shading or fine structures.

Cooperative Segmentation

Why would we care about homogenous label transitions and higher-order potentials? A common approach to segmenting images is to formulate the problem as inference in a Markov Random Field (MRF) or Conditional Random Field (CRF) with "attractive potentials". This is mathematically equivalent to saying that the image is a grid graph, where each pixel is a node, and we cut out the object from the grid. The penalty we pay is the length of the cut, i.e., the length of the object boundary. Obviously, this encourages segmentations with short boundaries. But not all natural objects have short boundaries:

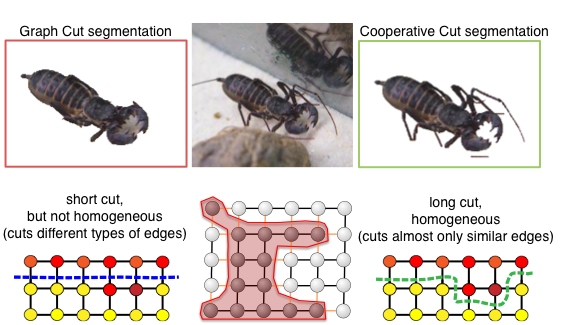
How could we then identify a correct boundary? In many cases, the true boundary might have complex shape, but it is fairly uniform (congruous): the inside (object) colors as well as the background pattern do not change all that much. Therefore, cooperative cut models penalize boundary length only if the boundary is diverse, i.e., non-uniform.

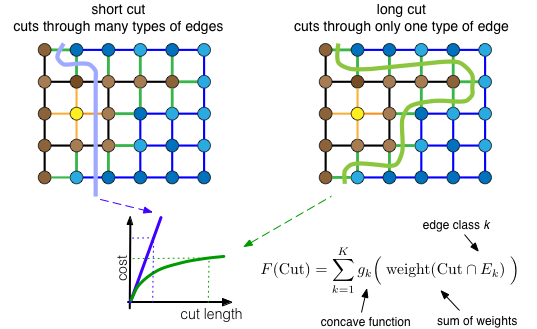
How is this achieved? We group the edges in the grid graph into classes of similar edges (similarity is determined from the color, intensity or other features of the adjacent nodes). We then have a submodular function over the edges that gives a discount if we use lots of edges from the same class - the cost increase diminishes as we cut more and more edges from the same class. But for each new class of edges that occurs in the cut, we must pay. Therefore, the cost of the blue cut below increases linearly with its length, and the cost of the green cut gets discounts.

Formally, the standard graph cut function counts the sum of edge weights

.

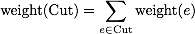The submodular cut function looks at each edge class $E_k$ separately (one term in the sum for each class). Within each class, it counts the edge weights like the standard function, and then squashes them with a concave function $g_k$:

.

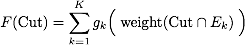As a result, this function favors the continuation of similar boundaries over short-cuts, and helps to better segment fine structures. The inference can be done by an iterative graph cut method, as described in the paper.

This also works for grayscale images, if we group edges by the ratios of the intensities of adjacent pixels:

Authors

• Evan Shelhamer, UC Berkeley CS / ICSI. @shelhamer
• Stefanie Jegelka, UC Berkeley CS / ICSI.
• Trevor Darrell, UC Berkeley CS / ICSI.